PID 제어는 현대 제어 시스템에서 핵심적인 역할을 하는 피드백 제어 알고리즘이다.
제어과정에서 발생하는 오차를 줄이고, 안정성을 확보하는데 중요한 도구이다.
드론 개발 과정에서도 중요하게 사용된다.
💡1. PID 제어기
PID 제어기(Proportional-Integration-Differential controller)는
피드백(Feedback) 제어기의 형태를 띈다.
아래의 그림은 PID 제어의 도식도이다.
- 제어 대상의 출력(output)을 측정해 목표하는 값인 설정값(setpoint)와 비교하여 오차(error)를 계산한다.
- 제어에 필요한 제어량(PID gain 값들)을 도출된 오류값을 이용해 계산한다.
- 각각 P(비례), I(적분), D(미분) 제어기를 의미한다

아래의 그림은 PID 제어기를 사용해 출력을 조정한 결과를 그래프로 나타낸 것이다.

🔍2. PID 제어 개념
2-1. 제어량 계산식
시간에 따른 제어량의 계산식은 다음과 같다.
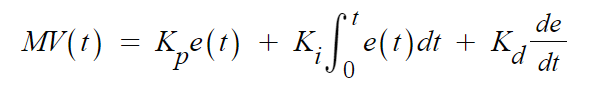
이를 라플라스 영역에서의 전달함수로 나타내면 다음과 같다.
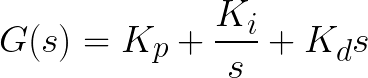
1. 비례 제어기(Proportional controller)

현재 제어값의 오차(error)에 비례한다. 현재 상태에서 오차의 크기에 따라 제어신호가 달라진다.
2. 적분 제어기(Integral controller)
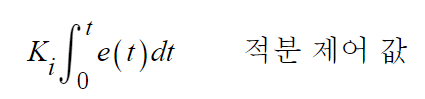
오차값의 적분(integral)에 비례한다. 정상 상태(Steady-state)에서의 오류를 없앤다.
3. 미분 제어기(Derivative controller)

오차값의 미분(derivative)에 비례한다. 출력값의 급격한 변화를 막아 오버슈트를 줄이며 안정성(stability)을 향상시킨다.
수식에서 e(t)라는 값이 나오는데, 이는

즉 e(t) = (제어량 - 목표값) 으로, 편차에 해당한다.
2-2. 이득값(Gain)
위의 제어량 계산식에서 Kp, Ki, Kd를 이득값(Gain)이라고 한다. 각각 비례 제어, 적분 제어, 미분 제어를 조절하는 계수이다.
이를 활용하여 특정 항만 가지는 제어기도 존재한다.
비례 제어기만 사용하는 P제어기, 비례-적분 제어기만 사용하는 PI제어기 등의 방식이다.
🔧3. 튜닝(Tuning)
튜닝(Tuning) 이란 앞서 언급했던 이득값(gain)을 수학적/경험적/실험적으로 계산하여 조정하는 것을 말한다.
적절한 게인값을 찾아야 정확하고 안정적으로 시스템을 제어할 수 있다.
PID 제어를 할때 모델에 대한 정보가 아예 없을 경우 사용할 수 있는 방법에는 지글러-니콜라스 방법이 있다.
이 방법으로 Kp, Ti, Td에 대한 값을 얻을 수 있다.
이는 추후에 설명하겠다.
🚥4. 제어 매커니즘
4-1. P(비례) 제어

P제어는 현재 제어값과 목표값의 차이(error)에 비례하여 제어량을 변화시키는 방법이다.
오차가 크면 조작량을 크게하여 제어량을 빠르게 증가시키지만, 오차가 작아질수록 조작량을 작게하여 제어량을 목표값에 유연하게 도달시킨다.
Kp 값을 크게 하면 편차에 따른 조작량이 크므로, 상승시간(rise time)이 줄어 빠르게 목표값에 도달할 수 있다.
대신 오버슈트(overshoot) 값이 크고 시스템에 무리를 줄 수 있다.
Kp
값이 작으면 제어 시스템은 더 느리게 목표값에 도달하게 된다.
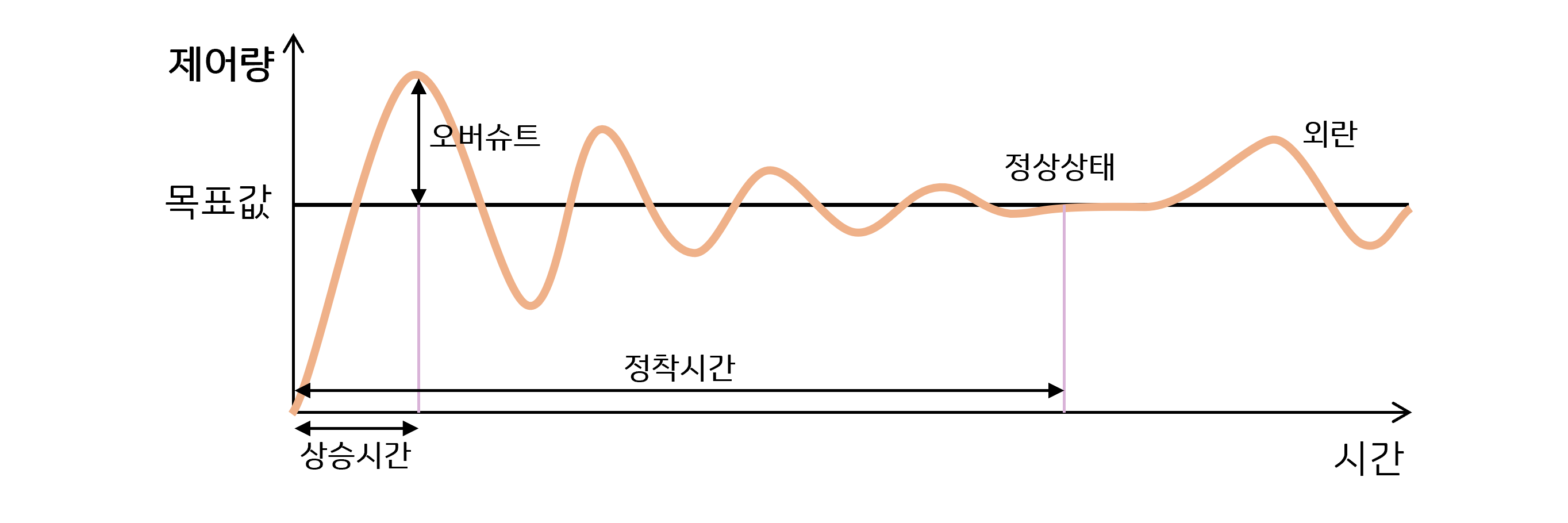
📌오버슈트(Overshoot)와 Peak time
- 오버슈트는 제어량이 목표값을 넘어가는 양(혹은 그 현상)을 말한다. 오버슈트 값이 커지면 시스템에 무리를 줄 수 있다.
예를 들어, 제어하는 대상이 전압이라면 오버슈트가 과전압을 초래할 수 있는 것이다.
반대 개념은 언더슈트(undershoot)이다.
처음 오버슈트에 도달하는데 걸리는 시간을 peak time 이라고 한다.
📌정상 상태(Steady-state)와 정착 시간
- 정상 상태는 제어량이 목표값에 거의 가까워진 상태이며, 정착시간이란 처음부터 정상상태가 될 때 까지 소요되는 시간이다.
제어를 할때 완벽하게 제어량을 목표량과 일치하게 만들 수 없기 때문에, 목표값 기준으로 일정% 범위 내에 제어값이 위치하게 된다면 제어가 되었다고 본다.정착시간이 짧을 수록 좋은 제어 시스템이라고 판단한다.

여기서 P 제어의 단점은 정상상태 오차(Steady-state error)가 남는다는 것이다.
정상상태 오차는 정상상태에 도달했으나, 끝까지 없어지지 않는 잔류 오차를 말한다.
정상상태 오차가 만들어지는 이유는 다음과 같다.
제어값이 목표값에 가까워지면 편차가 줄어들기 때문에 조작량 또한 점점 줄어든다.
하지만 줄어든다 해도 제어값 = 목표값은 되지 않아 항상 편차가 존재하게 된다.
ex) 초기값의 90%씩을 감소하는 형태로 목표값에 다가간다고 할때 처음 100의 값이 들어오면 90이 줄어들어 10만 남고 다시 90%가 줄어들면 1이 남고 또 90%가 줄어들면 0.1만 남고 0.01, 0.001...
즉 목표값으로 수렴하는 형태이다.
그렇기 때문에 그래프는 목표값에 한없이 다가가는 형태로 그려지게 되는 것이다.
4-2. I(적분) 제어
P제어에서 발생한 정상상태 오차(Steady-state error)를 제거하기 위해 I 제어를 도입할 수 있다.
I(적분)제어는 오차를 시간에 대해 누적(적분)하고, 이 누적값이 특정 값을 넘어서면 조작량을 증가시켜 오차값을 없앤다.
이 방법으로 좀 더 정밀하게 목표값에 도달할 수 있다.

위의 그림을 보면 오차를 적분한 값이 특정 값을 넘어선 이후에 I 제어가 시작하게 된다.
Ki 값이 커질수록 오버슈트가 커지며 상승시간이 짧아진다. Ki 값이 너무 커지면 발산하게 된다.
Ki 값이 작아지면 더 느리게 목표값에 도달하며 P 제어만 할 때보다 진동 없이 기준입력 점에 도달하여 안정된다.
I 제어의 문제점은 다음과 같다.
P 제어의 단점인 정상상태 오류를 제거할 수 있는 대신 정착시간(settling time)이 길어진다.
심지어 Ki 값이 클수록 오버슈트/언더슈트 값이 커지고 정착시간은 더 늘어난다.
외란(Disturbance) 발생시 반응 속도(응답시간)가 느려지는 것도 문제점이다. I 제어를 통해 편차에 대한 조작량을 작게 해두었으므로, 외란으로 인해 제어량 변화가 급작스럽게 커져도 조작량 변화는 작을 수밖에 없다. 더군다나 편차를 시간 단위로 측정하므로 외란 신호를 다시 목표값 부근으로 복원시키는 데 시간이 오래 걸린다. 즉, 응답시간이 오래 걸린다.
또한 외란이나 오차의 누적이 계속된다면 Ki에 의한 값이 커져 제어량의 발산이 유발될 수도 있다. 누적에 의한 발산을 막기 위해 적분 값을 초기화하는 등 anti-wind up 기법을 사용하기도 한다.
4-3 D(미분) 제어
D(미분) 제어는 목표량과 제어량의 편차를 비교해 이와 반대되는 쪽(기울기)으로 조작하는 방식이다. (편차)=+10이라면 (조작량)=-10이 되도록 조작 방향을 설정하는 식이다. 미용실에서 머리를 할 때, 미용사가 한 쪽으로 머리를 잡아당기면 우리는 반대쪽으로 힘을 주는 것과 같은 이치이다. 급격히 어느 한 방향으로 힘이 쏠리면 반대방향으로 힘을 주어 그 힘을 상쇄하려는 제어이다.
외란과 목표값의 편차, 혹은 이번 편차와 직전 편차를 비교해 이 크기에 따라 조작량을 결정하며, D 제어를 통해 외란에 대한 응답성을 개선하고 안정성을 높일 수 있다. 미분값은 미래의 값을 알 수 없으므로, 물리적으로 구현할 수 없는 제어이기도 하다.
목표값에 다가가다가, 이대로면 설정값을 초과할 것 같아 제어값의 변화에 대해 그것을 억제하는 작업으로 이해해도 좋다. 이대로 가속 페달을 밟다가는 목표 속도인 60km/h를 넘어버릴 것 같아 페달에서 발을 조금씩 떼는 식이다.

※ 짧은 샘플링 시간이나 갑작스런 외란이 미분값을 급작스럽게 변화시킬 수도 있으므로 보통 앞에 저주파 필터(Low-pass filter)를 붙여 사용하기도 한다.
값이 클수록 안정화에 걸리는 시간이 줄어들어 정착시간이 감소된다. 다만 정상상태에서는 D 제어보다 PI 제어의 영향이 크므로 이 구간에서 정상상태 오차의 변화는 거의 없다.
P, I 제어의 경우 편차와 같은 방향으로 제어량을 조작시키므로 게인 값과 오버슈트값은 비례하고 상승 시간이 반비례했다. 그러나 D 제어는 편차와 반대 부호로 조작을 하기 때문에, 값이 클수록 오버슈트는 감소하고 오차를 빨리 교정해, 상승시간과 정착 시간이 감소한다.
반대로 오차기준으로 생각하였을 때,
- 오차의 변화가 크지 않다면 미분항에 의해 D 제어값은 작으며 전체 제어값에 큰 영향을 주지 않는다.
- 오차의 변화가 갑자기 커진다면 미분항에 의해 D 제어값은 커지며 전체 제어값이 크게 변하는 경우를 막아준다.
D 제어의 장점은 오버슈트 값을 줄일 수 있다는 점이다.
제어 시스템이 전체적으로 민감해지고 불안정해 질 수 있다는 단점도 존재한다.
신호가 급변하는 경우, 시스템을 망가트릴 수도 있다.
4-4. PID 제어
PID 제어에서 각 제어의 역할은 다음과 같다.
- P 제어: 목표값 도달 시간 감소. 목표값과 멀수록 많이, 가까울수록 적게 조작.
- I 제어: 정상 상태 오차 감소. 목표값에 딱맞게 주행하기 위해 미세하게 조정하여 정상상태 오류 제거.
- D 제어: 오버슈트 억제. 제어값 변화 억제.
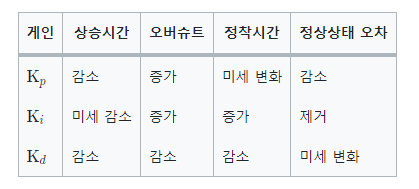
P-gain 증가: 반응속도(출력의 변화속도) 빨라짐.
I-gain 증가: 오버슈트 증가, 정상상태 오차 감소.
D-gain 증가: 오버슈트 감소, 수렴이 느리지만 안정적임.

이상적인 제어 결과
- 가장 이상적인 제어 결과는
- 빠른 응답속도를 가지며,
- 오버슈트가 발생하지 않고,
- 정상상태 오차가 발생하지 않는 것.
- gain값 사이의 trade-off 때문에 현실적으로 가능하지 않음.
- 따라서 적절히 타협을 보아야 함.
- 타협의 기준을 ()%이하의 오버슈트, ()sec의 정착시간 등으로 설정함.
- 주로 5%이내의 오버슈트, 0.2초내의 정착시간을 설정함.
제어기(Controller)를 거쳐 최종적으로 변화시키는 값 u은 다음과 같이 다시 쓸 수 있다.

각 항을 로 묶었을 때 나오는 는 Integral Time, 는 Derivative Time이라고 한다. 맨 마지막 식을 Matlab 등의 시뮬레이션 툴에서 많이 사용한다.
인용한 글 출처 :
https://kocoafab.cc/make/view/418
http://www.selco.kr/PIDcontrol.pdf
https://pus0319.github.io/embedded_control/PIDCONTROL/
https://alswo471.tistory.com/entry/PID-%EA%B0%9C%EB%85%90
https://monglory.tistory.com/48
https://blog.naver.com/proscw/221285498257
https://velog.io/@d2h10s/%EC%A0%9C%EC%96%B4%EA%B3%B5%ED%95%99-PID-%EC%A0%9C%EC%96%B4
https://mokhwasomssi.tistory.com/49
https://blog.naver.com/msnayana/220147585681
